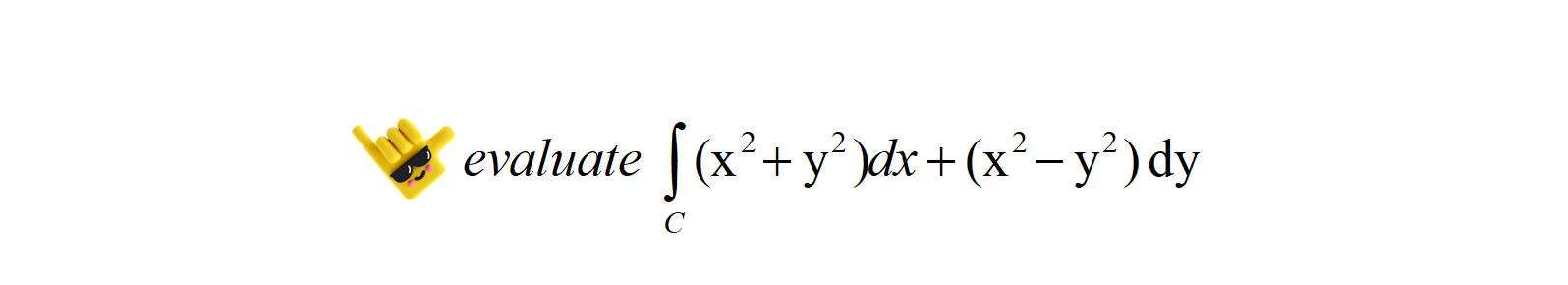Discussion of Green's Theorem (3)

1 Question:

Evaluate

$$\int_C\frac{xdy-ydx}{\pi(x^2+y^2)},$$

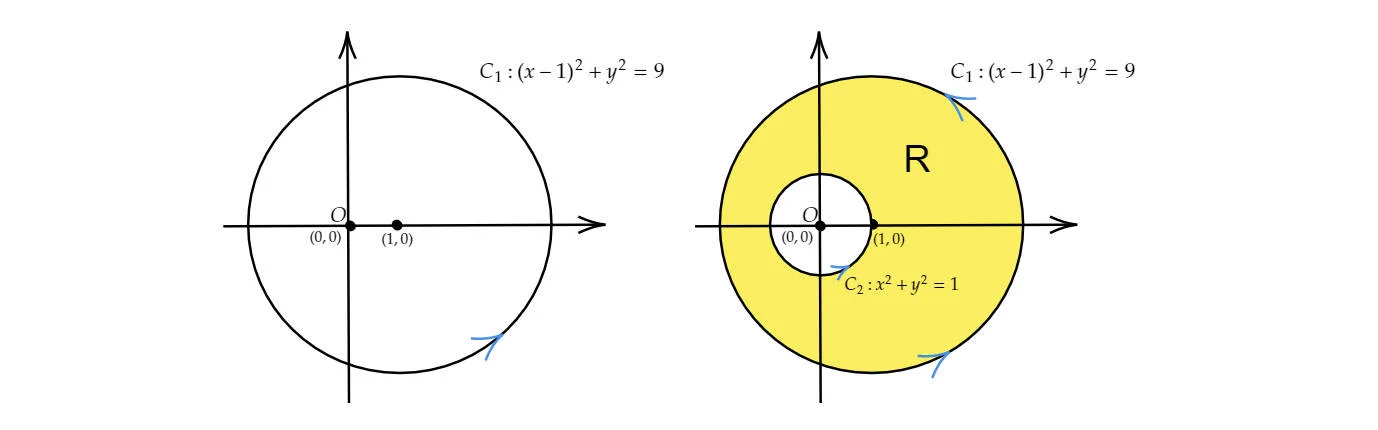
where $C_1$ is the circle $(x-1)^2+y^2=9$, traced in the anti-clockwise direction.

2 Discussion:

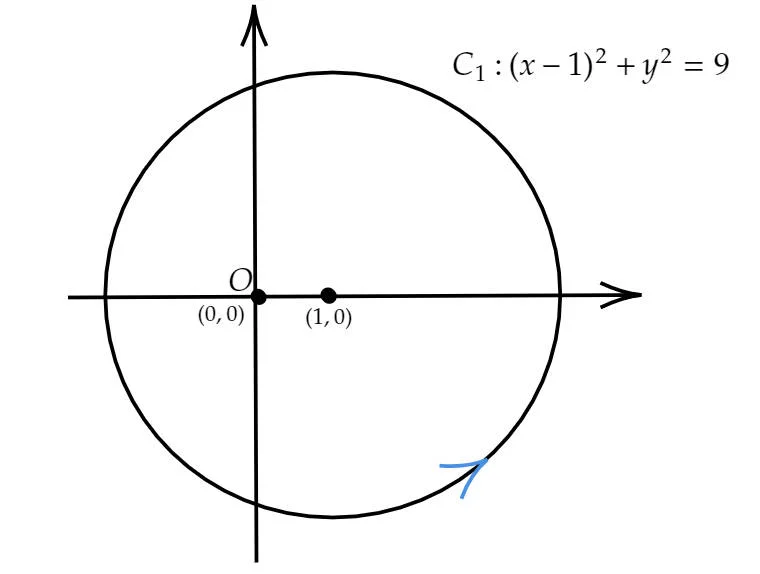
Since the curve $C_1$ is given by $(x-1)^2+y^2=9$, then the corresponding domain $D$ enclosed by $C$ is:

$$D=\{(x,y): (x-1)^2+y^2\le9\},$$

which is a disc without any holes.

The corresponding diagram is as below:

Next,

$$ \int_C\frac{xdy-ydx}{\pi(x^2+y^2)}=\frac{1}{\pi}\int_C \begin{pmatrix} \frac{-y}{x^2+y^2}\\ \frac{xdy}{x^2+y^2} \end{pmatrix} \cdot \begin{pmatrix} dx\\ dy \end{pmatrix} =\frac{1}{\pi}\int_C F \cdot dr, $$

where $F=\begin{pmatrix}\frac{-y}{x^2+y^2}\\ \frac{x}{x^2+y^2}\end{pmatrix}=\begin{pmatrix}P\\ Q\end{pmatrix}$, $dr=\begin{pmatrix} dx\ dy\end{pmatrix}$, and $r=r(t)$ is the parametric equation of the curve $C$.

Note that $F$ is undefined at $(x,y)=(0,0)$.

2.1 Idea 1:

Recall, for a vector field $F$, the line integral of $F$ along $C$ is

$$\int_C F \cdot dr =\int_a^b F(r(t)) \cdot r'(t)\,dt.$$

For this problem, $r(t)=\begin{pmatrix}1+3\cos t\\ 3\sin t\end{pmatrix}, 0 \leq t \leq 2\pi$, and hence,

$$\int_C\frac{xdy-ydx}{\pi(x^2+y^2)}=\frac{1}{\pi}\int_C F \cdot dr =\frac{1}{\pi}\int_0^{2\pi} \begin{pmatrix} \frac{-3\sin t}{(1+3\cos t)^2+(3\sin t)^2}\\\ \frac{1+3\cos t}{(1+3\cos t)^2+(3\sin t)^2}\end{pmatrix} \cdot \begin{pmatrix} -3\sin t\\\ 3\cos t\end{pmatrix}\,dt=...,$$

Theoretically, this method should work,but in practice,as you see the above definite integral is too complicated to handle, so let’s try to figure out some other ideas.

2.2 Idea 2:

Assume $ F=\begin{pmatrix}P\\ Q\end{pmatrix}$. We know $F$ is undefined at $O(0,0)$, and then it’s easy to check $P_y=Q_x$ when $(x,y)$ is on the domain $D$ except the origin $O(0,0)$.

Thus, by the test for the conservative vector field, $F$ is conservative on $D$ except $(0,0)$, NOT on the whole region $D$ or for the each point of region $D$.

Hence, Fundamental Theorem of Line integrals is NOT applicable here, which is, we can not perform

$$\int_C F \cdot dr = f(r(b))-f(r(a)).$$

2.3 Idea 3:

As $F$ is undefined at $O(0,0)$,the actual domain of integration in this problem should be

$$D^*=\{(x,y): (x-1)^2+y^2\le9, \text{and } (x,y) \neq (0,0)\},$$

which is a disc with a hole,and we call it non-closed. Hence, Green’s Theorem can NOT be applied directly in this case. So what else shall we do? We can draw a unit circle, $i.e. C_2:x^2+y^2=1$ , where the little hole $O(0,0)$ is within this circle, as shown in the following diagram:

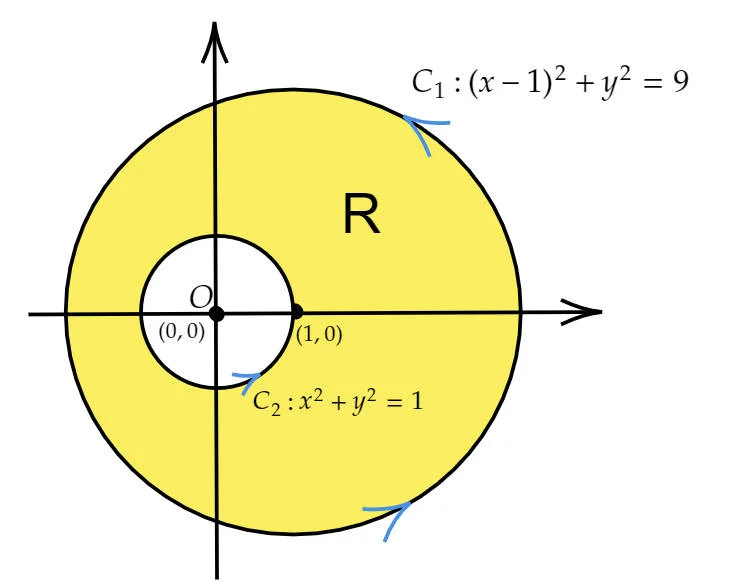
Where R is is the region between $C_1$ and $C_2$, and the boundary of $R$ is $\partial R=C_1-C_2$

By the Green’s Theorem,

$$\oint_{\partial R} F \cdot dr =\iint_R (Q_x-P_y)dx =0,$$

as $P_y=Q_x$ is conservative on the region $R$.

$\implies \int_{C_1-C_2} F \cdot dr =0$, $\implies \int_{C_1}F \cdot dr =\int_{C_2}F \cdot dr=2$,based on the result obtained in the last post,say the Discussion of Green’s Theorem (2).

3 Credit:

The question is from Dr. Tuan Seng Chew.